Chapter 03 手写数字识别

本章承接上一章，在又一个经典问题用三种算法让大家了解开发者是怎么样工作的。

禁止转载，侵权必究！

MNIST问题

MNIST是经典的机器学习问题，它的目标是通过学习50000张28×28像素的黑白图片的手写数字，让程序能够自动识别图片中的数字。我们会通过百度的AI Studio给大家演示整个过程。

识别目标

下图是我用鼠标在Photoshop中画的数字8，我期望训练好的机器学习程序能够帮助我识别出来。

公用代码

import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
import os
from PIL import Image
import gzip
import json
import random

加载数据的python代码

# 定义数据集读取器
def load_data(mode='train'):

    # 数据文件
    datafile = './work/mnist.json.gz'
    print('loading mnist dataset from {} ......'.format(datafile))
    data = json.load(gzip.open(datafile))
    train_set, val_set, eval_set = data

    # 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
    IMG_ROWS = 28
    IMG_COLS = 28

    if mode == 'train':
        imgs = train_set[0]
        labels = train_set[1]
    elif mode == 'valid':
        imgs = val_set[0]
        labels = val_set[1]
    elif mode == 'eval':
        imgs = eval_set[0]
        labels = eval_set[1]

    imgs_length = len(imgs)

    assert len(imgs) == len(labels), \
          "length of train_imgs({}) should be the same as train_labels({})".format(
                  len(imgs), len(labels))

    index_list = list(range(imgs_length))

    # 读入数据时用到的batchsize
    BATCHSIZE = 100

    # 定义数据生成器
    def data_generator():
        if mode == 'train':
            random.shuffle(index_list)
        imgs_list = []
        labels_list = []
        for i in index_list:
            img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
            label = np.reshape(labels[i], [1]).astype('int64')
            imgs_list.append(img) 
            labels_list.append(label)
            if len(imgs_list) == BATCHSIZE:
                yield np.array(imgs_list), np.array(labels_list)
                imgs_list = []
                labels_list = []

        # 如果剩余数据的数目小于BATCHSIZE，
        # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
        if len(imgs_list) > 0:
            yield np.array(imgs_list), np.array(labels_list)

    return data_generator

1. 模型MNIST_A

我们用类的方式来定义模型。在这里我们仍然采用波士顿房价预测的模型：fc = Linear(线性全连接模型)。

# 定义线性预测全连接单层网络 MNIST_A
class MNIST(fluid.dygraph.Layer):
    def __init__(self):
        super(MNIST, self).__init__()
        
        # 定义一层全连接层，输出维度是1，激活函数为None，即不使用激活函数
        self.fc = Linear(input_dim=784, output_dim=1, act=None)
        
    # 定义网络结构的前向计算过程
    def forward(self, inputs):
        outputs = self.fc(inputs)
        return outputs

用训练集训练模型

# MNIST_A
with fluid.dygraph.guard():
    model = MNIST()
    model.train()
    train_loader = load_data('train')
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，格式需要转换成符合框架要求的
            image_data, label_data = data
            # 将数据转为飞桨动态图格式
            image = fluid.dygraph.to_variable(image_data.reshape(100, 784))
            label = fluid.dygraph.to_variable(label_data.astype('float32'))
            
            #前向计算的过程
            predict = model(image)
            
            #计算损失，取一个批次样本损失的平均值
            loss = fluid.layers.square_error_cost(predict, label)
            avg_loss = fluid.layers.mean(loss)
            
            #每训练了1000批次的数据，打印下当前Loss的情况
            if batch_id  % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()

    # 保存模型
    fluid.save_dygraph(model.state_dict(), 'mnist')

训练结果

loading mnist dataset from ./work/mnist.json.gz ......
epoch: 0, batch: 0, loss is: [27.73817]
epoch: 0, batch: 200, loss is: [5.5403943]
epoch: 0, batch: 400, loss is: [4.6792817]
epoch: 1, batch: 0, loss is: [5.6096168]
epoch: 1, batch: 200, loss is: [5.7397876]
epoch: 1, batch: 400, loss is: [4.560763]
epoch: 2, batch: 0, loss is: [4.5133085]
epoch: 2, batch: 200, loss is: [4.1860423]
epoch: 2, batch: 400, loss is: [4.4305124]
epoch: 3, batch: 0, loss is: [3.5777836]
epoch: 3, batch: 200, loss is: [4.327017]
epoch: 3, batch: 400, loss is: [3.7929125]
epoch: 4, batch: 0, loss is: [3.6808846]
epoch: 4, batch: 200, loss is: [3.6938505]
epoch: 4, batch: 400, loss is: [4.122206]

可以看到这个模型训练是很快的。我们知道损失函数loss是越小越好，但是这个模型的损失函数明显是降不下来的。也就是说用单层全连接Linear模型来处理手写数字识别问题是不合适的。我们进一步看看手工测试的结果。

下面是用来手工验证模型的python代码

# 手工测试效果 MNIST_A
def load_image(img_path):
    # 从img_path中读取图像，并转为灰度图
    im = Image.open(img_path).convert('L')
    im = im.resize((28, 28), Image.ANTIALIAS)
    im = np.array(im)
    print(im.shape)
    im = im.reshape(1, 784).astype(np.float32)
    # 图像归一化，保持和数据集的数据范围一致
    im = 1.0 - im / 255.
    print(im.shape)
    return im

# 定义手工测试过程
with fluid.dygraph.guard():
    model = MNIST()
    params_file_path = 'mnist'
    # img_path = './work/example_0.png'
    img_path = './work/number8.png'
# 加载模型参数
    model_dict, _ = fluid.load_dygraph("mnist")
    model.load_dict(model_dict)
# 灌入数据
    model.eval()
    tensor_img = load_image(img_path)
    result = model(fluid.dygraph.to_variable(tensor_img))
#  预测输出取整，即为预测的数字，打印结果
    print("本次预测的数字是", result.numpy().astype('int32'))

下面是运行的结果

(28, 28)
(1, 784)
本次预测的数字是 [[6]]

我用Photoshop画的是8，预测结果是6，显然不对。

2. 模型MNIST_B

通过模型MINIST_A的问题，我们想到一些改进方法：

1. 采用多层网络
2. 采用新的激活函数sigmoid（非线性函数）

# 多层全连接神经网络实现 MNIST_B
class MNIST(fluid.dygraph.Layer):
    def __init__(self):
        super(MNIST, self).__init__()
        # 定义两层全连接隐含层，输出维度是10，激活函数为sigmoid
        self.fc1 = Linear(input_dim=784, output_dim=10, act='sigmoid') # 隐含层节点为10，可根据任务调整
        self.fc2 = Linear(input_dim=10, output_dim=10, act='sigmoid')
        # 定义一层全连接输出层，输出维度是1，不使用激活函数
        self.fc3 = Linear(input_dim=10, output_dim=1, act=None)
    
    # 定义网络的前向计算
    def forward(self, inputs, label=None):
        inputs = fluid.layers.reshape(inputs, [inputs.shape[0], 784])
        outputs1 = self.fc1(inputs)
        outputs2 = self.fc2(outputs1)
        outputs_final = self.fc3(outputs2)
        return outputs_final

用训练集训练模型

#MNIST_B
with fluid.dygraph.guard():
    model = MNIST()
    model.train()
    #调用加载数据的函数，获得MNIST训练数据集
    train_loader = load_data('train')
    # 使用SGD优化器，learning_rate设置为0.01
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
    # 训练5轮
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据
            image_data, label_data = data
            image = fluid.dygraph.to_variable(image_data)
            label = fluid.dygraph.to_variable(label_data.astype('float32'))
            
            #前向计算的过程
            predict = model(image)
            
            #计算损失，取一个批次样本损失的平均值
            loss = fluid.layers.square_error_cost(predict, label)
            avg_loss = fluid.layers.mean(loss)
            
            #每训练了200批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()

    #保存模型参数
    fluid.save_dygraph(model.state_dict(), 'mnist')

训练结果

loading mnist dataset from ./work/mnist.json.gz ......
epoch: 0, batch: 0, loss is: [38.411476]
epoch: 0, batch: 200, loss is: [6.3446875]
epoch: 0, batch: 400, loss is: [4.647622]
epoch: 1, batch: 0, loss is: [4.027138]
epoch: 1, batch: 200, loss is: [3.4333525]
epoch: 1, batch: 400, loss is: [3.5657587]
epoch: 2, batch: 0, loss is: [3.8097577]
epoch: 2, batch: 200, loss is: [2.6363297]
epoch: 2, batch: 400, loss is: [2.6171744]
epoch: 3, batch: 0, loss is: [2.5799212]
epoch: 3, batch: 200, loss is: [2.4907866]
epoch: 3, batch: 400, loss is: [3.331763]
epoch: 4, batch: 0, loss is: [1.8398556]
epoch: 4, batch: 200, loss is: [1.7335011]
epoch: 4, batch: 400, loss is: [1.626342]

我们发现训练速度还是比较快的。我们用两层的全连接非线性模型，可以看到loss比MNIST_A要好。那么我们仍然看看手工验证的结果：

# 手工测试效果 MNIST_B
def load_image(img_path):
    # 从img_path中读取图像，并转为灰度图
    im = Image.open(img_path).convert('L')
    im = im.resize((28, 28), Image.ANTIALIAS)
    im = np.array(im)
    print(im.shape)
    im = im.reshape(1, 1, 28, 28).astype(np.float32)
    # 图像归一化，保持和数据集的数据范围一致
    im = 1.0 - im / 255.
    print(im.shape)
    return im

# 定义手工测试过程
with fluid.dygraph.guard():
    model = MNIST()
    params_file_path = 'mnist'
    img_path = './work/example_0.png'
    # img_path = './work/number8.png'
# 加载模型参数
    model_dict, _ = fluid.load_dygraph("mnist")
    model.load_dict(model_dict)
# 灌入数据
    model.eval()
    tensor_img = load_image(img_path)
    result = model(fluid.dygraph.to_variable(tensor_img))
#  预测输出取整，即为预测的数字，打印结果
    print("本次预测的数字是: ", result.numpy().astype('int32'))

下面是运行结果

(28, 28)
(1, 1, 28, 28)
本次预测的数字是:  [[6]]

结果还是不对，我们要怎么做呢？

3. 模型MNIST_C

思考一下成语故事盲人摸象。有的盲人摸到了鼻子，有的盲人摸到了耳朵，有的盲人摸到了腿，综合大家的结果，可以猜出来是大象。行业内解决图片识别的常用方法是CNN（卷积神经网络）也是这个原理。

CNN用卷积conv来扫描和学习特征，用池化pooling删除部分特征，减少神经连接数。我们可以做以下优化：

1. 从Linear网络升级为CNN网络
2. sigmoid激活函数改为relu激活函数
3. 使用交叉熵cross_entropy代替均方差square_error_cost计算loss
4. 使用softmax函数输出10个标签

# 卷积神经网络  MNIST_C
class MNIST(fluid.dygraph.Layer):
     def __init__(self):
         super(MNIST, self).__init__()
         
         # 定义一个卷积层，使用relu激活函数
         self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
         # 定义一个池化层，池化核为2，步长为2，使用最大池化方式
         self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
         # 定义一个卷积层，使用relu激活函数
         self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
         # 定义一个池化层，池化核为2，步长为2，使用最大池化方式
         self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
         # 定义一个全连接层，输出节点数为10 
         self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
    # 定义网络的前向计算过程
     def forward(self, inputs):
         x = self.conv1(inputs)
         x = self.pool1(x)
         x = self.conv2(x)
         x = self.pool2(x)
         x = fluid.layers.reshape(x, [x.shape[0], 980])
         x = self.fc(x)
         return x

用训练集训练模型

# #MNIST_C
with fluid.dygraph.guard():
    model = MNIST()
    model.train()
    #调用加载数据的函数
    train_loader = load_data('train')
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
    EPOCH_NUM = 5
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，变得更加简洁
            image_data, label_data = data
            image = fluid.dygraph.to_variable(image_data)
            label = fluid.dygraph.to_variable(label_data)
            
            #前向计算的过程
            predict = model(image)
            
            #计算损失，使用交叉熵损失函数，取一个批次样本损失的平均值
            loss = fluid.layers.cross_entropy(predict, label)
            avg_loss = fluid.layers.mean(loss)
            
            #每训练了200批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()

    #保存模型参数
    fluid.save_dygraph(model.state_dict(), 'mnist')

训练结果：

loading mnist dataset from ./work/mnist.json.gz ......
epoch: 0, batch: 0, loss is: [2.63713]
epoch: 0, batch: 200, loss is: [0.414802]
epoch: 0, batch: 400, loss is: [0.27256364]
epoch: 1, batch: 0, loss is: [0.23372334]
epoch: 1, batch: 200, loss is: [0.25631276]
epoch: 1, batch: 400, loss is: [0.16240163]
epoch: 2, batch: 0, loss is: [0.08554713]
epoch: 2, batch: 200, loss is: [0.12564537]
epoch: 2, batch: 400, loss is: [0.11252453]
epoch: 3, batch: 0, loss is: [0.16606194]
epoch: 3, batch: 200, loss is: [0.12781247]
epoch: 3, batch: 400, loss is: [0.14138581]
epoch: 4, batch: 0, loss is: [0.125189]
epoch: 4, batch: 200, loss is: [0.06888349]
epoch: 4, batch: 400, loss is: [0.11047111]

训练速度是很慢的，但是我们发现改过之后loss值明显变小了。我们仍然手工验证一下模型：

# 手工测试效果 MNIST_C
def load_image(img_path):
    # 从img_path中读取图像，并转为灰度图
    im = Image.open(img_path).convert('L')
    im = im.resize((28, 28), Image.ANTIALIAS)
    im = np.array(im)
    print(im.shape)
    im = im.reshape(1, 1, 28, 28).astype(np.float32)
    # 图像归一化，保持和数据集的数据范围一致
    im = 1.0 - im / 255.
    print(im.shape)
    return im

# 定义手工测试过程
with fluid.dygraph.guard():
    model = MNIST()
    params_file_path = 'mnist'
    # img_path = './work/example_0.png'
    img_path = './work/number8.png'
# 加载模型参数
    model_dict, _ = fluid.load_dygraph("mnist")
    model.load_dict(model_dict)
# 灌入数据
    model.eval()
    tensor_img = load_image(img_path)
    result = model(fluid.dygraph.to_variable(tensor_img))
    lab = np.argsort(result.numpy())
    # result = model(fluid.dygraph.to_variable(tensor_img))
#  预测输出取整，即为预测的数字，打印结果
    # print("本次预测的数字是", result.numpy().astype('int32'))
    print("debug result", result.numpy())
    print("本次预测的数字是: ", lab[0][-1])

手工验证结果：

(28, 28)
(1, 1, 28, 28)
本次预测的数字是:  8

OK，我们的模型MNIST_C终于能正确识别手写数字了。

基本原理的通俗化解释

为什么要引入这些函数？

答：手写数字识别问题数学上是一个多分类问题。需要用到概率函数。然而概率函数并非是代数，计算机并不容易计算，为了方便计算所以需要引入sigmoid，relu，softmax这些函数。

为什么要用多层网络？

答：取决于问题的复杂性，现实问题不可能总是简单到单层网络可以学习。

为什么要使用激活函数？

答：我们想象一下，在手写数字和背景的边界是不是一个突变。为了学习这种突变，我们用sigmoid显然会更好，因为sigmoid函数图就是一个突变。同理relu函数来自脑科学，而且它的突变特性比sigmoid更好。如图：

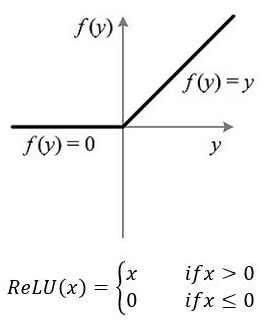
为什么要改成CNN网络？

全连接（full connection）网络有两个问题：

1. 我们把28×28像素的图像当做784像素的一维数组输入到了模型中。这显然不符合实际。因为图片像素点是有位置关系的。
2. fc网络要计算每个像素和其他像素点权重值，实际上像素点只跟周围的像素点有关系，这显然不符合常理。但是卷积conv使用”点积”神经网络，正好符合现实情况。

为什么要加入softmax函数？

答：它别名归一化指数函数，它把所有的x归结到[0,1)之间，且所有x之和为1。这些特性和分类问题非常匹配。[0,1)是非负数，而且加和又为1。非常方便计算。比如：做手写数字分类时，只要把output设置为10维，0~9每个数字对应softmax中的一维，代码非常好写。

为什么要用交叉熵cross_entropy替代均方差square_error_cost？

答：cross_entropy表示预测概率值与实际概率值之差，这个差值越小，它的值最小。所以我们最小化loss就是最小化cross_entropy函数的值。分类问题本质是概率分布问题，在分类问题中使用它显然比square_error_cost更好。

示例代码

源码地址

评估CPU/GPU算力消耗

paddle-paddle 卷积向下取整，池化向上取整。

1. Paddle 1.8.x版本

经过实验，我们得到了正确模型，但是我也说到，训练速度很慢。那么慢在哪里呢？我们先看看第一层卷积的代码：

self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')

• num_channels 输入通道个数
• num_filters 输出特征图（feture map）个数，输出通道个数
• filter_size 卷积(滤波器)大小，5表示：5 x 5
• stride 步长
• padding 填充(避免卷积后图片变小)
• batch_size 100张图片

输入数据形状(100, 1, 28, 28) 。卷积K（滤波器）5×5 输出通道20 步长stride=1 填充padding=2

拿conv2D函数类比线性函数 y = wx +b, 那么学习参数w的形状(Cout, Cin, Kh, Kw) = ( 20, 1, 5, 5); b的形状等于Cout = 20； 输出特征图FeatureMap形状(Hout, Wout) = ( Hin + 2 x padding – Kh + 1, Win+ 2 x padding – Kw +1 ) = (28, 28) ,所以输出的形状(N, C, H, W) = ( 100, 20, 28, 28 )

2. Paddle 2.x版本

官方API定义如下：

paddle.nn.Conv2D(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, padding_mode=’zeros’, weight_attr=None, bias_attr=None, data_format=’NCHW’)

• in_channels (int) – 输入图像的通道数。
• out_channels (int) – 由卷积操作产生的输出的通道数。
• kernel_size (int|list|tuple) – 卷积核大小。

输入数据形状(100, 1, 28, 28) 。卷积核K 5×5 输出通道20 步长stride=1 填充padding=2

输出FeatureMap（Hout, Wout）= 28 + 2 x 2 -5 + 1 ,xxx = (28,28),输出形状(N, C, H, W) = (100, 20, 28, 28)

3. 所需CPU/GPU算力为：

单个像素卷积算力 = 对5 x 5的矩阵做点积运算，并加上偏置项b。结果是25×2=50次（乘法和加法各25次）

总算力 = Cin x 单个像素卷积算力 x 输出形状 = 1 x 50 x (100 x 20 x 28 x 28) = 78,400,000

所以我们对一个批次的MNIST数据(28px * 28px)做一层卷积计算量就达到了惊人的8千万次。

深入了解数据的形状

Conv2D计算

层	w形状	w参数个数	b形状	b参数个数	输出形状
conv1	(20,1,5,5)	500	(20)	20	(100,20,28,28)

Pool2D计算

self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

• pool_size 池化核Kh x Kw， 2表示2 x 2
• pool_padding 默认值为0
• pool_stride 步长
• pool_type “max”表示最大池化算法

(Hout, Wout) = ( (Hin- Kh + 2 x pool_padding) / stride + 1, (Win- Kw + 2 x pool_padding) / stride + 1 ) = ( ( 28 – 2 + 2 x 0 )/2 +1, ( 28 – 2 + 2 x 0 )/2 +1 ) = ( 14, 14 )。简而言之：输出减半。

层	w形状	w参数个数	b形状	b参数个数	输出形状
pool1	–	–	–	–	(100,20,14,14)

MNIST_C完整的形状变化

层	w形状	w参数个数	b形状	b参数个数	输出形状
conv1	(20,1,5,5)	500	(20)	20	(100,20,28,28)
pool1	–	–	–	–	(100,20,14,14)
conv2	(20,20,5,5)	10000	(20)	20	(100,20,14,14)
pool2	–	–	–	–	(100,20,7,7)
Linear	(980,10)	9800	(10)	(10)	(100,10)

最后输出100张图片，每张图片有10个分类(0~9)。