目录
前言
人工智能已经很牛了,但是智慧生物可以在没有监督的情况下探索自己的环境并学习有用的技能(skill),以后面临特定任务时,他们可以使用这些技能(skill)快速有效地完成。
不依赖reward(学习skill)有几个实际的应用场景。比如:在稀疏奖励情况下,如果agent没有探索到目标,那么很长一段时间是无法获得奖励的,无监督学习skill就适用于这个场景。对于长任务,分层RL(简称 HRL)中skill是必备的因素。而且一些模拟环境中,可以无限尝试,但是获取奖励的代价比较高。学习skill可以提高训练效率,因为设计奖励函数在一些情况下极具挑战。而且,在陌生的环境中,找到哪些任务本身就是一个挑战。无监督学习skill可以部分解决这个问题。
skill的本质是什么?
skill是一种潜在的条件策略,可以稳定的改变环境状态。因为奖励函数未知,求解公式就转化为最大化skill集合,且要求skill尽可能不同(diversity)并且尽可能大地探索环境状态空间。本论文论述了一个基于互信息让agent自主求解skill集合的方法。在很多场景,比如HRL中就很有效。
google原BLOG: Diversity is all you need
一、算法原理
三个原则:
- 要用skill来决定agent访问的状态
- 要用状态和skill来定义公式,而不是动作。因为不产生状态变化的动作是不可观察的。
- 鼓励探索尽可能多的技能,越随机越好。高熵的skill为了区分自己应该去探索远离其他skill的状态空间。
我们用了信息论的符号来书写公式:
- S 状态
- A 动作
- Z ∼ p(z) 隐藏变量,条件策略;我们将以固定Z为条件的策略称为skill
- I (·; ·) 互信息
- H[·] 香农熵
算法要最大化I(S;Z)。I(A;Z)表示用skill来决定agent访问哪个状态,为了确保用skill而不是动作,我们要最小化I(A; Z|S)。把p(z)看成混合策略集合,最大化它的香农熵H(A|S)。公式(1)如下:
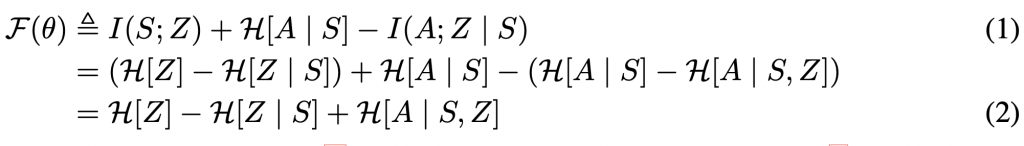
公式(2)是根据信息论从公式(1)推导而来,以简化算法的目标。
公式(2)第一项表示要最大化p(z)上的香农熵,在算法中我们固定了p(z)以保证它的熵最高。第二项求S状态下触发skill的最小熵,这个计算很容易。第三项求S状态下,用了skill触发动作的最大熵。实际上状态S的所有策略集合的p(z|s)是无法计算的,那么我们只能用学习到的判别器(discriminator)qφ(z | s)近似后验值。Jensen不等式告诉我们用qφ(z | s)代替p(z|s)可以得到目标函数F(θ)的变分下界G(θ, φ),推到过程如下:
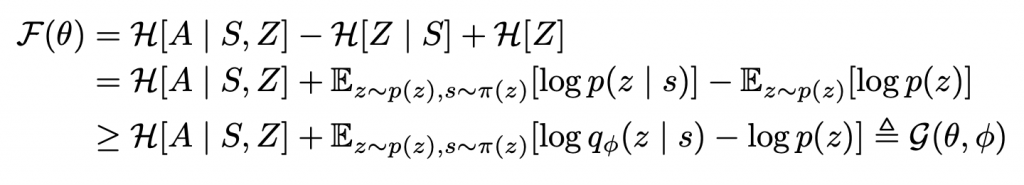
二、技术实现
我们利用算法SAC来实现的DIAYN,学习针对z的策略πθ (a | s, z)。SAC是在动作A上最大化策略π,跟目标函数G中的熵相关。我们用α来缩放熵正则化子H[a | s,z]。实验证明α=0.1在探索性和可辨别性之间较为平衡。为了最大化G,我们用下面公式的奖励替代任务奖励:
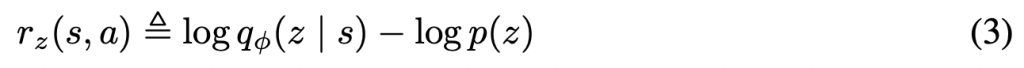
我们对p(z)使用了分类分布。无监督学习过程中我们从p(z)抽样z,在整个过程中都使用这个skill z。agent访问可区分的states而得到奖励,同时判别器(discriminator)被更新,正则化熵作为SAC算法的一部分被更新。如下图:

三、算法稳定性
跟之前的提出的对抗性非监督学习算法不同,DIAYN是合作性的非监督学习算法。避免了对抗性非监督学习的“鞍点不稳定性”。在连续动作和近似设置下,算法对收敛性有较高要求,但是即使像DQN这样的近似算法也不能保证一定收敛,即便如此算法仍然是有效的。算法对随机种子有较好的鲁棒性。
附:相关阅读
信息论的来源:克劳德·香农的著作《A Mathematic Theory of Communication》。熵代表着系统的混乱程度,而优化算法就是不断减少这个“混乱程度”。
信息量(Information Quantity):
为什么信息量是对数函数,比如抛掷硬币3次,我们知道所有可能性是2的3次方(指数函数)共8种组合(不是2*3=6种组合)。因此当我们知道p,求n(也就是上式中的τ)就要用指数函数的反函数log。
举例:“2026国足会踢进世界杯。” 这句话信息量就非常大,因为概率非常小(-log0.01 = 2)。而反过来说2026国足踢不进世界杯,就没有什么信息量(-log0.9=0.045757)。
对于一个给定分布:
随机变量X的信息熵(Information Entropy)为:
仔细对比上面公式可以发现:信息熵(Information Entropy)就是信息量(Information Quantity)的数学期望E。