L-DAE解构扩散模型实现自监督学习

可随意转载 Update 2024.02.08

前言

来自KaiMing大神2024年1月的论文《Deconstructing Denoising Diffusion Models for Self-Supervised Learning》

摘要

我们研究了去噪扩散模型（Denoising Diffusion Models，DDM）的表示学习能力，它最初是为图像生成而设计的。我们的想法是解构它，逐步将它转换为经典去噪自编码器（Denoising Autoencoder，DAE）。解构过程可帮助大家探索DDM的组件是如何影响自监督学习。我们发现，大部分组件对于自监督学习都是非必需的。研究得到了一个极简的算法，与经典的DAE很相似。我希望此项研究能够重新激发人们对自监督学习的经典算法的兴趣。

一、简介

去噪算法是当前CV领域的热门生成算法。被称为DDM的这些算法，它们学习了一个DAE[39]，该编码器通过扩散过程去除多级噪声。这些算法在生成高质量的图像，特别是高分辨率、逼真的图像方面取得了令人印象深刻的效果。这些生成模型如此出色，以至于普遍认为它们似乎具有强大的识别表示能力，能够理解视觉内容。

理论上DAE是DDM生成模型的源头，但DAE最初的形式是以自监督学习的方式从数据中学习表示[39]。在表示学习社区中，当前较为成功的DAE们形式上都是”masking nosie”[39]的方法，如预测缺失的文本（例如，BERT [10]）或预测缺失的图像（例如，MAE [21]）。在概念上，这些masking nosie形式的DAE们与去噪的DDM们明显不同：mask标记了未知内容，而去噪模型中不存在这样的标记。因此用于生成的DDM模型主要基于去噪方法，这意味着它们在没有标记的情况下学习表示。

研究者近来越来越关注DDM的表示学习能力[40，28]。特别要提到，这些研究通常使用现成的预训练DDM[23，32, 11]，评估它们对识别的表示质量。他们报告了令人鼓舞的结果。然而，这些开创性的研究显然留下了一些未解决的问题：这些预训练DDM模型是为生成而设计的，而不是为识别而设计；到底是去噪过程还是扩散过程产生了表示能力仍然没弄清楚。

本论文对近期的研究方向进行了深入的探索。我们并未使用现成的DDM预训练模型，而是训练自己的面向识别的模型。我们的核心理念是解构DDM算法，逐步将其转变为经典的DAE。通过这种解构研究，我们以表征学习为目标，审视了DDM的每一个方面。这一研究增强了我们对DAE学习表征能力的理解。

我们发现关键组件之一居然是创建隐空间（降维）的tokenzier[33]。实验结果显示它与tokenizer的具体实现算法无关——我们研究了多种tokenizer，例如：标准VAE[26]，Patch-VAE，Patch-AE和Patch-PCA编码器等。我们发现使得DAE能够达到良好表征的是隐空间本身，而非哪种tokenizer。

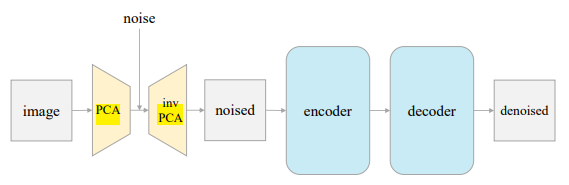
由于PCA的有效性，解构过程最终达到了一个与经典DAE（图1）极为相似的简单架构。我们使用Patch-PCA将图像投影到一个隐空间，添加噪声，然后通过逆PCA将其投影回来。然后我们训练一个自编码器来预测去噪后的图像。我们将这种架构称为“Latent Denosing AutoEncoder”（L-DAE）。

解构过程还揭示了许多其他DDM和经典DAE之间的引人入胜的属性。比如，我们发现即使使用单一的噪声水平（即，不使用DDM的噪声调度）也可以使用我们的L-DAE得到一个相当不错的结果。使用多种噪声的方法的本质是一种类似数据增强的方法，有用但并不是一个强因子。有了这些观察结果，我们认为DDM的表征能力主要是通过去噪过程得到的，而非扩散过程。

最后，我们将我们的结果与先前的基线进行比较。一方面，我们的结果显著优于基线（遵循[40，28]的精神）：这是预期之内的，因为我们把这个基线当做了解构工作的起点。另一方面，我们的结果不及基于对比学习的方法（如[7]）和基于掩码的方法（如[21]），但差距已经缩小。我们的研究表明，DAE和DDM的方向还有更多的研究空间。我们的研究结果，虽然在一些方面不及基于对比学习方法和基于掩码的方法，但在缩小这些差距方面已经取得了一定的进展。通过这个研究表明DAE和DDM有更多的研究潜力。

二、相关工作

在ML和CV的历史中，图像生成领域与无监督（自督学习）的发展紧密相连。生成算法在概念上是无监督（自监督）学习的形式，模型无需标记数据进行训练，学习捕捉输入数据的基础分布。

有一种普遍的观点，即：模型生成高保真度数据的能力，表明其具有学习良好表征的潜力。例如，生成对抗网络（GAN）[18]引发了对对抗表征学习[13，12]的广泛兴趣。变分自编码器（VAEs）[26]最初被概念化为用于近似数据分布的生成模型，现已发展成为学习局部表征（“令牌”）的标准，例如VQVAE[30]和其变体[16]。图像修复[2]，本质上是一种有条件的图像生成形式，已经导致了一系列现代表征学习方法，包括上下文编码器（Context Encoder）[31]和遮罩自编码器（MAE）[21]。

类似地，去噪扩散模型（DDM）[36，37，38，23，11]的出色生成性能引起了人们对其在表征学习中的潜力的关注。当前的前沿研究[40，28]通过对DDM预训练模型来进行。然而，我们注意到，虽然模型的生成能力表明了一定程度的理解能力，但并不一定能转化为对下游任务有用的表征。本研究深入探讨了这些问题。

另一方面，尽管DAE[39]为基于自编码的表征学习奠定了基础，但它们主要局限于有Mask的场景（例如，[21，41，17，5]）。据我们所知，几乎没有研究报告了带有denoising的DAE变体，其中的根本原因是DAE基线过于简单（图2（a）），因此表现不佳（例如，在∼20%的图5中）。

三、背景：DDM

解构性研究始于DDM[36, 37, 38, 23, 11]。我们简要描述我们使用的DDM，参照[11, 32]。

扩散过程从一个干净的数据点（z0）开始，逐步添加噪声。在指定的时间步长t，噪声数据z_t由公式给出：

z_t = γ_tz₀ + σ_tϵ 公式1

其中ϵ∼N (0, I)是从高斯分布采样的噪声映射，γ_t和σ_t分别定义了信号和噪声的缩放因子。默认情况下，设置γ_t² + σ_t² = 1 [29, 11]。

DDM训练目标是学习去噪，条件是时间步长t。与原始DAE[39]预测干净输入不同，DDM[23, 29]通常预测噪声ϵ。具体来说，这种形式的损失函数被最小化：

∥ϵ − net(z_t)∥² 公式2

其中net(z_t)是网络输出。网络针对给定噪声时间表的多个噪声级别进行训练，以时间步长t为条件。在生成过程中，训练模型被反复应用，直到达到干净的信号z₀。

DDM可以在两种类型的输入空间上运行。一个是原始的像素空间[11]，其中原始图像x₀直接用作于z₀。另一个选择是在由tokenizer生成的隐空间上构建DDM，参照[33]。见图2(b)。在这种情况下，预训练tokenizer f(通常是AE，例如VQVAE[30])被用来将图像x₀映射到其在隐空间的表示z₀=f(x₀)。

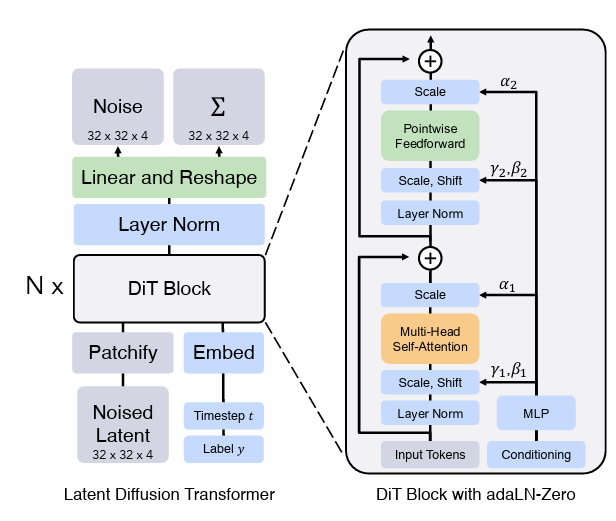
Diffusion Transformer(DiT) 我们的研究从DiT[32]开始。我们选择这个基于Transformer的DDM有以下几个原因：

(i) 与其他基于UNet的DDM[11, 33]不同，基于Transformer的架构可以与其他的Transformer自监督学习基线（例如[7, 21]）进行更公平的比较；

(ii) DiT在编码器和解码器之间有更清晰的区别，而UNet的编码器和解码器通过跳跃连接实现，在评估编码器时需要增加额外的工作；

(iii) DiT在实现更好的生成质量的同时，训练的速度比其他基于UNet的DDM快得多（见[32]）。

我们使用DiT-Large（DiT-L）变体[32]作为我们的DDM基线。在DiT-L中，编码器和解码器一起具有ViT-L [15]（24个块）的大小。我们评估编码器的表示质量（线性探测精度），它有12个块，被称为“1/2L”（半大）。分词器。在[32]中实例化的DiT是潜在扩散模型(LDM) [33]的一种形式，它使用了一个VQGAN分词器[16]。具体来说，这个VQGAN分词器将256×256×3的输入图像（高度×宽度×通道）转换为一个32×32×4的潜在映射，步幅为8。

起始基线。默认情况下，我们在ImageNet[9]上训练模型400个周期，分辨率为256×256像素。实现细节在Sec. A中。

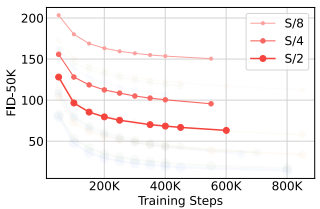
我们的DiT基线结果在Tab. 1 (line 1)中报告。使用DiT-L，我们报告了其1/2L编码器的线性探测精度为57.5%。这个DiT-L模型的生成质量（Frechet Inception Distance [22], FID-50K）为11.6。这是我们破坏性轨迹的起点。

尽管在实现细节上存在差异，但我们的起点在概念上遵循了最近的研究[40, 28]（更具体地说，是DDAE [40]），这些研究在线性探测协议下评估了现成的DDM。

DiT是Facebook公司做的基于Transformer（而不是Unet）架构的扩散生成模型，github地址。

DiT论文的中文翻译。

四、解构DDM

我们的解构过程分为三个阶段。首先，我们调整DiT中以生成为中心的设置，使其更加倾向于自监督学习（第4.1节）。接着，我们逐步解构和简化tokenizer设计（第4.2节）。最后，我们尽可能地逆转许多DDM驱动的设计，将模型推向经典的DAE[39]（第4.3节）。我们在第4.4节总结了从这个解构过程中得到的经验。

4.1. 将DDM的目标从生成调整为自监督学习

虽然DDM在概念上是DAE的一种形式，但它最初是为了图像生成的目的而开发的。DDM中的许多设计都是面向生成任务的。有些设计在自我监督学习中是不合法的（例如，涉及到类标签）；如果不关心图像质量，有些设计是不必要的。在这个小节中，我们修改DDM基线，让它以自监督学习为目标，总结在下表中。

注：L-DAE这篇论文不是讲怎么生成高质量的图片的，如果读者目的是生成高质量图片，不需要浪费时间看了

移除class-conditioning 高质量的DDM通常在class标签下进行训练，因为这可以大大提高生成质量。但在我们的自我监督学习研究中，class标签的使用不合适。作为第一步，我们在基线中移除class标签。

令人惊讶的是，移除class条件显著提高了线性探测精度，从57.5%提高到62.1%(Tab. 1)，尽管如我们所预期的，生成质量大大降低（FID从11.6降到34.2）。我们假设在class标签上对模型进行conditioning可能会降低模型对编码与class标签相关信息的需求。移除class可以迫使模型学习更多的语义。

注：这里提到了一个经验，高质量的扩散模型通常是带class标签训练的，这里没有解释所谓线性探测精度（linear probe accuracy）是什么。

解构VQGAN 在我们的基线中使用了由LDM [33]提出并由DiT继承的VQGAN tokenizer，经由多个损失项训练：

（i）自动编码重构损失；

（ii）KL散度正则化损失 [33]；2

（iii）基于监督的VGG网络 [35] 的感知损失，该网络经过ImageNet分类训练；

（iv）带有鉴别器的对抗性损失 [18,16]。

我们在表1中去除了后两项。

由于感知损失 [44]涉及到一个经过监督预训练的网络（通常是VGG16），使用感知损失函数训练的VQGAN是不合适的。相反，我们训练了另一种VQGAN tokenizer [33]，故意去掉了感知损失。使用这个tokenizer会明显降低线性探测器的准确率，从62.5%降到58.4% (表1)，然而，这提供了迄今为止的第一个合规条目。这个比较揭示了，一个与感知损失（带类标签）一起训练的tokenizer本身就提供了语义表征。我们注意到，感知损失从现在开始，在本文的剩余部分将不再使用。

我们训练了下一个VQGAN tokenizer，进一步去除了对抗损失。它稍微提高了线性探测器的准确率，从58.4%提高到59.0% (表1)。至此，我们的tokenizer本质上是一个VAE，我们将在下一小节中对其进行解构。我们还注意到，去除任何一种损失函数都会损害生成质量。

替换噪声调度 在生成任务中，目标是逐步将噪声转化为图像。因此，在非常嘈杂的图像上花费了许多时间步（图3）。如果我们的模型不是面向生成的，那么这就没有必要。 我们研究了一个更简单的噪声scheduler用于自监督学习。具体来说，我们让γ_t²在1>γ_t²≥0的范围内线性衰减（图3）。这允许模型在更清晰的图像上花费更多的时间步。这种改变大大提高了线性探测器的准确率，从59.0%提高到63.4% (表1)，这表明原始 scheduler 过于关注噪声较大的地方。另一方面，正如预期的那样，这样做进一步损害了生成能力，导致FID为93.2。

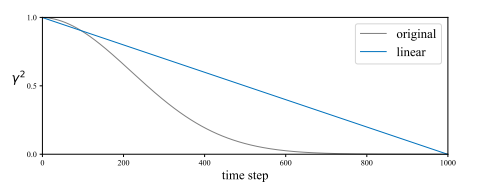
总结 总的来说，表1中的结果揭示了自监督学习的性能并不与生成质量相关。DDM的表示能力并不一定是其生成能力的结果。

注：FID表示保真度，它影响生成质量，去掉这些后FID上升了（越大越差），但是线性探测精度（linear probe accuracy）反而上升了。

4.2. 解构Tokenizer

接下来，我们通过做出重大简化，进一步解构VAE tokenizer。我们比较了以下四种作为tokenizer的自动编码器变体，每一种都是前一种的简化版本：

1. 卷积VAE 首先是VAE tokenizer。按照常规做法 [26, 33]，这个VAE的编码器f(·)和解码器g(·)都是深度卷积神经网络 [27]。这个卷积VAE最小化以下损失函数：

∥x − g(f(x))∥ ² + KL [f(x)|N ]

这里，x是VAE的输入图像。第一项是重构损失，第二项是f(x)的隐分布与标准高斯分布之间的Kullback-Leibler散度 [3, 16]。

2. Patch-VAE 考虑简化上述tokenizer，假如VAE的编码器和解码器都是线性投影（linear projections），其中输入x是图像patch（参考ViT论文），我们得到了新的tokenizer：Patch-VAE，最小化它的损失函数：

∥x − U ^T V x∥ ² + KL [V x|N ]

这里，x表示一个被拍平成D维的patch。U和V都是d×D矩阵，其中d是隐空间的维度。我们将patch大小设置为16×16像素（按照 ViT论文设置）。

注：一个16×16的patch，那么拍平后的D=16×16 = 256 维

3. Patch-AE 我们在VAE上进一步简化，去除了上式中的正则化项：

∥x − U ^T Vx ∥ ²

因此，这种tokenizer本质上是在图像patch上的一个自编码器(AE)，其中编码器和解码器都是线性投影。

4. Patch-PCA 最后，我们考虑一个更简单的变体，它在块空间上执行主成分分析（PCA）。可以轻易地证明，PCA等同于AE的一个特殊情况： ∥x – V^T V x∥²。 其中V满足V V^T = I (d×d的单位矩阵)。 PCA基可以简单地通过对大量随机采样的块进行特征值分解来计算，无需基于梯度的训练。

由于使用块的简单性，对于这三个块状标记器，我们可以在块空间中可视化他们的过滤器（图4）。

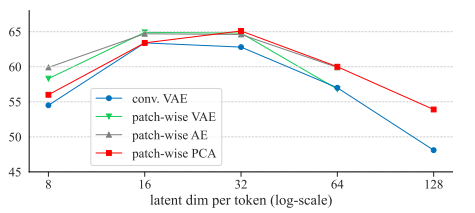
表2总结了使用这四种变体标记器的DiT线性探测精度。显示了与每个token的隐维度相关的结果，因此， 我们得出以下观点:

1. 隐维度(latent dimension)对DDM在自监督学习中的良好运行至关重要。

如表2所示，尽管四种变体的tokenizer在架构和损失函数上有所不同，但它们展示出相似的趋势。有趣的是，最佳隐维度相对较低（d为16或32），尽管每个patch的完整维度要高得多（16×16×3=768）。

令人惊讶的是，在我们的研究中卷积VAE作为tokenizer既不必要也不受欢迎；相反，所有基于patch的 tokenizer ，每个patch都是独立编码的，它们的表现相似并始终优于Conv VAE变体。此外，KL正则化项是不必要的，因为AE和PCA变体都工作得很好。

让我们进一步惊讶的是，即使PCA tokenizer 也表现良好。与VAE或AE对应的 tokenizer 不同，PCA tokenizer 不需要基于梯度的训练。有了预计算的PCA基础，PCA tokenizer 的应用类似于图像预处理的一种形式，而不是“网络架构”。PCA tokenizer 的有效性在很大程度上帮助我们将DDM推向经典DAE，我们将在下一小节中展示。

注：简单说，研发去噪自编码器（DAE）卷积，变分这些玩意都不用；Patch方法无需预训练模型和GPU，更快更好。

2. 基于图像高分辨率的DDM对于自监督学习来说是不好的。

在我们继续之前，我们报告了一个与前述观察一致的额外消融。具体来说，我们考虑一个“天真的 tokenizer ”，它在从resized的图像中提取的patch上执行identity mapping。在这种情况下，“token”是包含一个patch的所有像素的扁平化向量。

在下图5中，我们展示了这种“基于像素”的tokenizer的结果，它在256、128、64和32的像素尺寸(对应16、8、4、2的patch尺寸)上操作。这个空间的隐维度分别为768、192、48和12（每token）。在所有情况下，Transformer的序列长度保持不变（256）。

注：16x16x3=768 8x8x3=192 4x4x3=48

有趣的是，这种基于像素的tokenizer显示出与我们研究过的其他分词器相似的趋势，尽管最优维度d有所偏移(基于像素的tokenizer最优维度是d=48，它对应于图像大小为64，patch大小为4)。当图像大小为256像素，patch大小为16 ，d=768时（对应上述隐空间的最优维度），线性探测精度显著下降到23.6%。

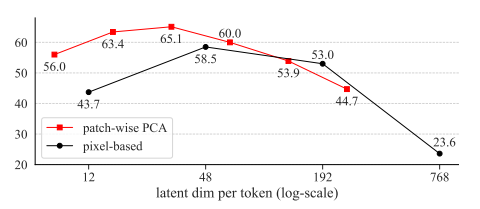
结论：不同的tokenizer和它们产生的隐空间在自监督学习场景（对于DDM/DAE）中的竞争力至关重要。特别的，将带有加性高斯噪声的经典DAE应用到原始像素空间会降低效果。

注：其他论文，例如google的论文（simple diffusion）所讲，在高分辨率下做扩散模型（参考本站文章），作者提出了不同的观点，并通过实验证明了隐空间对DAE的重要性。

4.3. 朝向经典的去噪自动编码器

接下来，我们将继续解构，目标是尽可能接近经典的DAE [39]。我们试图去除PCA-DDM和经典DAE之间的不同。通过这种解构过程，我们对每个现代设计可能如何影响经典DAE有了更好的理解。表3给出了结果，接下来进行讨论。

预测干净数据（而非噪声）虽然现代的DDM通常预测噪声ϵ，见公式（2），但经典的DAE却预测干净数据。我们通过最小化以下损失函数来检验这个差异：

λ_t ‖z₀ − net(z_t)‖² 公式3

在这里，z₀是干净数据（在隐空间中），net(z_t)是网络预测。λ_t是t依赖的损失权重，被引入来平衡不同噪声级别的贡献[34]。建议将λ_t设置为γ²_t /σ²_t，如[34]所示。我们发现在我们的情况下，将λ_t设置为γ²_t效果更好。直观地说，它只是增加了干净数据（更大的γ^t）的损失项的权重。

通过预测干净数据（而非噪声）的修改，线性探测的准确性从65.1%降低到62.4%（表3）。这表明预测目标的选择影响了表示质量。

尽管这一改动acc变差了，但我们将坚持这一修改，因为我们的目标是朝着经典的DAE前进。

移除输入缩放 在现代的DDMs中（参见公式（1）），输入被一个γ_t因子所缩放。这在经典的DAE中并不常见。接下来，我们研究移除输入缩放，即我们设定γ_t ≡ 1。由于γ^t是固定的，我们需要直接在σ_t上定义一个噪声调度。我们简单地设定σ_t为从0到√2的线性调度。此外，我们经验性地设定公式（3）中的权重为λ_t = 1/(1 + σ²_t)，这再次强调了对干净数据（较小的σt）的重视。 在固定γ_t ≡ 1之后，我们达到了63.6%的精度（表3），这与变化的γ_t对应物的62.4%相比是有利的。这表明在我们的场景中，通过γ_t缩放数据并不必要。

通过逆PCA在图像空间上操作 到目前为为止，我们探索的所有项目（除图5外），都在由tokenizer产生的隐空间上（图2（b））。理想情况下，我们希望DAE可以直接在原始图像上工作，同时仍然保持良好的精度。我们可以通过逆PCA实现这个目标。 这个想法在图1中被说明。特别的，我们通过PCA（例如：V）将输入图像投影到隐空间，然后在隐空间中添加噪声，并通过逆PCA（V^T）将隐空间噪声投影回原始图像。图1（中，下）显示了一个在隐空间中添加噪声的示例图像。有了这个噪声图像作为网络的输入，我们可以应用一个直接在图像上操作的标准ViT网络[15]，不用tokenizer。

在输入端应用这种修改（同时仍在隐空间预测输出）有63.6%的精度（表3）。进一步将其应用到输出端（即，在图像空间上使用逆PCA预测输出）有63.9%的精度。这两个结果都表明，通过逆PCA在图像空间上操作可以达到与在潜在空间上操作相似的结果。

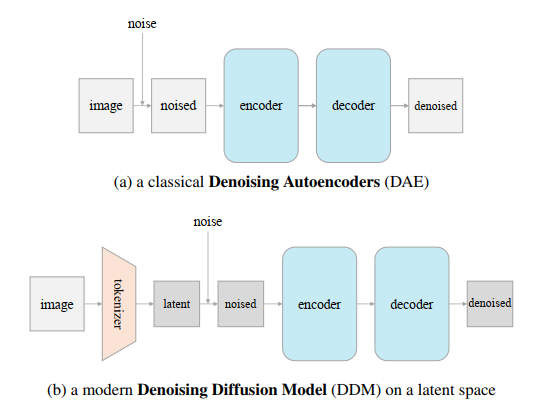
预测原始图像 虽然逆PCA可以在图像空间中产生预测目标，但这个目标并不是原始图像。这是因为对于任何减小的维度d，PCA都是一个损失编码器。相反，直接预测原始图像是一个更自然的解决方案。

当我们让网络预测原始图像时，引入的“噪声”包括两部分：（i）附加的高斯噪声，其内在维度为d和（ii）PCA重构误差，其内在维度为D – d (D 是768)。我们对这两部分的损失进行不同的权重。

形式上，对于清晰的原始图像x₀和网络预测net(x_t)，我们可以计算投影到全PCA空间的残差：r ≜ V (x₀ – net(x_t))。这里的V是表示全PCA的D-by-D矩阵。然后我们最小化以下损失函数：

λ_t ∑_i=1 ^Dw_ir²_i 公式4

这里i表示向量r的第i维。每维权重wi是1对于i ≤ d, 和0.1对于d < i ≤ D。直观上，w_i降低了PCA重构误差的损失。通过这种公式，预测原始图像可以达到64.5%的线性探测精度（表3）。这种变体在概念上非常简单：它的输入是噪声图像（其噪声是在PCA隐空间中添加的）目标是预测原始图像（图1）。

单一噪声级别 最后，出于好奇，我们进一步研究了单级噪声的变体。我们注意到，由噪声调度给出的多级噪声是由DDMs中的扩散过程所引发的属性；在经典的DAE中，它在概念上是不必要的。 我们将噪声级别σ固定为一个常数（p 1/3）。使用这种单级噪声可以达到61.5%的精度，比多级噪声对应物（64.5%）低3%。使用多级噪声类似于在DAE中对数据进行增强：它是有用的但不是关键因素。这也意味着DDM的表示能力主要是由去噪驱动的过程获得的，而不是一个扩散驱动的过程。

由于多级噪声是有用的并且在概念上简单，我们将其保留在我们在下一节中提出的最终条目中。

4.4 总结

总的来说，我们解构了一个现代DDM并将其推向经典的DAE（图6）。我们取消了许多现代设计，并且在概念上只保留了来自现代DDM的两个设计：

（i）用于添加噪声的低维隐空间

（ii）多级噪声的设计

我们使用表3末尾的条目作为我们最后的DAE实例（如图1所示）。我们将此方法称为“潜在去噪自动编码器”，简称为l-DAE。

五、分析与比较

可视化潜在噪声 从概念上讲，L-DAE是一种学习如何移除添加到隐空间噪声的DAE。由于PCA的简单性，我们可以通过逆PCA轻松地可视化隐空间的噪声。 图7比较了添加到像素和隐空间的噪声。与原始图像噪声不同，隐空间噪声大多不受图像分辨率的影响。使用patch-wise PCA作为tokenizer，隐空间噪声的模式主要由patch大小决定。直观地说，我们可能会将其视为使用patch，而不是像素，来解析图像。这种行为类似于MAE [21]，它会屏蔽掉patch而不是单个像素。

去噪结果 图8显示了基于l-DAE的更多去噪结果示例。尽管噪声很重，我们的方法仍能产生合理的预测。我们注意到，这并不令人惊讶，因为基于神经网络的图像恢复[4,14]一直是一个深入研究的领域。然而，可视化可能有助于我们更好地理解L-DAE如何学习良好的表征。隐空间添加的重噪声为模型解决问题创造了挑战。预测基于一个或几个嘈杂的patch在本地的内容是微不足道的（甚至对于人类），模型被迫学习更高级别、更整体的语义来理解底层的对象和场景。

数据增广

值得注意的是，到目前为止我们介绍的所有模型都没有数据增强：只使用了图像的中心剪裁，没有随机调整大小或颜色抖动，这是遵循[11，32]的做法。我们进一步探索了对最终的 l-DAE 的温和数据增强（随机调整大小的剪裁）：

增强 中心剪裁 随机剪裁

精度 64.5 65.0

这有所改善。这表明 l-DAE 的表示学习能力在很大程度上独立于其对数据增强的依赖性。在 MAE [21]中观察到了类似的行为，这与对比学习方法的行为（例如，[6]）有很大不同。

训练周期 到目前为止，我们的所有实验都基于400周期的训练。按照MAE[21]的步骤，我们也研究了800和1600周期的训练： 周期 400 800 1600 精度 65.0 67.5 69.6 作为参考，MAE [21]从400周期扩展到800周期有显著的增长（4%），而MoCo v3 [7]从300周期扩展到600周期几乎没有增长（0.2%）。

模型大小 到目前为止，我们所有的模型都基于DiT-L变体[32]，其编码器和解码器都是“ViT-1/2L”（ViT-L的一半深度）。我们进一步训练不同大小的模型，其编码器是ViT-B或ViT-L（解码器总是与编码器大小相同）： 编码器 ViT-B ViT-1/2L ViT-L 精度 60.3 65.0 70.9 我们观察到与模型大小有关的良好的缩放行为：从ViT-B缩放到ViT-L有10.6%的大增长。在MAE[21]中也观察到了类似的缩放行为，它从ViT-B到ViT-L有7.8%的增长。

与前期基准的比较 最后，为了更好地了解不同的自我监督学习方法的性能，我们在表4中与先前的基线进行比较。我们考虑MoCo v3 [7]，它属于对比学习方法的家族，和MAE[21]，它属于掩蔽基础方法的家族。有趣的是，L-DAE与MAE相比表现得相当不错，显示出1.4%（ViT-B）或0.8%（ViT-L）的差距。我们注意到，这里的训练设置在MAE和L-DAE之间尽可能公平：两者都训练了1600个周期，并以随机裁剪作为数据增强。另一方面，我们也应该注意，因为MAE只在未掩蔽的patch上操作，所以在训练中更有效率。然而，我们已经大大缩小了MAE和DAE驱动方法之间的精度差距。 最后，我们观察到，在这个协议下，基于自编码器的方法（MAE和L-DAE）与对比学习方法相比仍然落后，尤其是在模型较小的时候。我们希望我们的研究能引起更多关注自监督学习的自编码器基础方法的研究。

六、结论

我们的研究提出了L-DAE，它其在很大程度上类似于经典的DAE，在自监督学习中可以有竞争力的表现。关键的组成部分是一个低维隐空间，噪声就在这个空间中被添加。我们希望本研究将重新激发人们对于在今天的自监督学习中基于去噪的方法的兴趣。

代码实操

DiT

DiT来自论文《Scalable Diffusion Models with Transformers》，作者应该跟Facebook有关。

官方 PyTorch版的DiT实现中的Attention是来自HuggingFace timm库，修改DiT代码去除PyTorch DDP（一种多机多卡训练框架）相关代码实现单机单卡训练。使用Facebook的xformers库降低训练中显存消耗（安装xformers后timm库会自动应用设置，无需手动修改代码）后可以在24G显存上跑训练。

参考PyTorch 2.0加速Transformer，通过使用SDPA（PyTorch2.0以上版本）优化，优化后在24G显存中可以训练DiT-L/2模型（L表示Large，如果显卡更好可用XL；2表示patch数，越小越好），image batch_size=16。

class DiTBlock(nn.Module):
    """
    A DiT block with adaptive layer norm zero (adaLN-Zero) conditioning.
    """
    def __init__(self, hidden_size, num_heads, mlp_ratio=4.0, **block_kwargs):
        super().__init__()
        self.norm1 = nn.LayerNorm(hidden_size, elementwise_affine=False, eps=1e-6)
        self.attn = Attention(hidden_size, num_heads=num_heads, qkv_bias=True, **block_kwargs)
        self.norm2 = nn.LayerNorm(hidden_size, elementwise_affine=False, eps=1e-6)
        mlp_hidden_dim = int(hidden_size * mlp_ratio)
        approx_gelu = lambda: nn.GELU(approximate="tanh")
        self.mlp = Mlp(in_features=hidden_size, hidden_features=mlp_hidden_dim, act_layer=approx_gelu, drop=0)
        self.adaLN_modulation = nn.Sequential(
            nn.SiLU(),
            nn.Linear(hidden_size, 6 * hidden_size, bias=True)
        )

    def forward(self, x, c):
        shift_msa, scale_msa, gate_msa, shift_mlp, scale_mlp, gate_mlp = self.adaLN_modulation(c).chunk(6, dim=1)
        x = x + gate_msa.unsqueeze(1) * self.attn(modulate(self.norm1(x), shift_msa, scale_msa))
        x = x + gate_mlp.unsqueeze(1) * self.mlp(modulate(self.norm2(x), shift_mlp, scale_mlp))
        return x

Patch PCA

Patch-based PCA: 过完备（over-complete）字典和稀疏（sparse）表示技术在图像去噪应用中广泛应用，是目前最先进的去噪算法之一。他们能将噪声信号和真实图像信号分离，因此能抑制噪声并保留边缘，但是它们比较费内存和算力，Deledalle改进了这种算法提出了 基于Patch的主成分分析法 （PB-PCA）。它通过构造简单正交（orthogonal）字典降低了算法复杂度和算力消耗，它从噪声图像中学习正交字典，并学习字典中的Patch系数的阈值，类似小波去噪，使用硬阈值或者软阈值将系数归0。

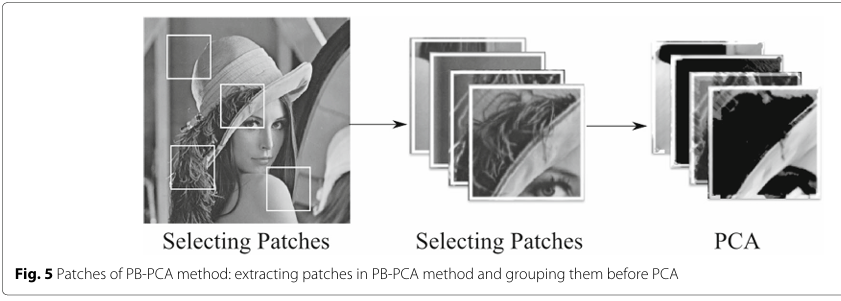
PCA计算使用了SVD方法分解，得到的特征向量（Eigenvectors）被称为数据的主成分轴（axis）。

PB-PCA产生了三种变体：PGPCA(全局)，PLPCA(局部)，PHPCA(层次)。

相关论文收集：

Deledalle等， 《Image denoising with patch based PCA: local versus global》，2011年

《Invertible Denoising Network: A Light Solution for Real Noise Removal》

PGPCA的python实现

代码包括PCA，逆PCA以及主成分轴的可视化。

# AGPL-3.0 license
# Author: ouyangshixiong
# Date: 2024-02-07

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from PIL import Image
import time
from PCA_utils import spatial_patchization, reprojection_UWA, psnr
def PGPCA_best_params(sigma):
    hP = 0
    factor_thr = 0
    if sigma == 5 or sigma == 10:
        hP = 7
        factor_thr = 2.50
    elif sigma == 20:
        hP = 7
        factor_thr = 2.75
    elif sigma == 40:
        hP = 12
        factor_thr = 2.75
    return hP, factor_thr

def hardthresholding(ima_ppca, threshold):
    coefs = np.where(np.abs(ima_ppca) > threshold, ima_ppca, 0)
    return coefs

def PGPCA_denoising(ima_patchs, threshold):
    m, n, p = ima_patchs.shape
    print("m={},n={},p={}".format(m,n,p))
    ima_patchs = ima_patchs.reshape((m*n, p))  # reshape image patches to 2D
    pca = PCA()
    ima_ppca = pca.fit_transform(ima_patchs)

    # Plot the first 16 principal components
    # fig, axes = plt.subplots(4, 4, figsize=(10, 10))
    # for i, ax in enumerate(axes.flat):
    #     if i < 16:
    #         ax.imshow(pca.components_[i].reshape((WP, WP)), cmap='gray')
    #         ax.set_title(f"Principal Component {i+1}")
    #     ax.axis('off')
    # plt.show()

    ima_ppca_fil = hardthresholding(ima_ppca, threshold)
    ima_patchs_fil = pca.inverse_transform(ima_ppca_fil)
    ima_patchs_fil = ima_patchs_fil.reshape((m, n, p))  # reshape image patches back to original shape
    return ima_patchs_fil, ima_ppca_fil


np.random.seed(2)  # 设置随机数种子
sigma=10  # 噪声等级

# 读取图像并转化为灰度图像
ima = np.array(Image.open('data/barbara.png').convert('L'), dtype=np.double)
# 添加高斯噪声
ima_nse = ima + sigma * np.random.randn(*ima.shape)

# 显示噪声图像
plt.figure(figsize=(8, 8))
plt.imshow(ima_nse, cmap='gray')
plt.title(f'Noisy: \n  PSNR {psnr(ima, ima_nse):.2f}')
plt.show()

# 计算最佳参数
WP, factor_thr = PGPCA_best_params(sigma)
threshold = factor_thr * sigma

start_time = time.time()  # 开始计时
# 将图像划分为块
ima_patchs, ima_normalization = spatial_patchization(ima_nse, WP)
# 对每个块进行PCA降噪
ima_patchs_fil, ima_ppca_fil = PGPCA_denoising(ima_patchs, threshold)
# 将处理后的块重新组合成图像
ima_fil_PGPCA = reprojection_UWA(ima_patchs_fil)
end_time = time.time() - start_time  # 结束计时

# 显示降噪后的图像
plt.figure(figsize=(8, 8))
plt.imshow(ima_fil_PGPCA, cmap='gray')
plt.title(f'PGPCA: \n  PSNR {psnr(ima, ima_fil_PGPCA):.2f}')
plt.show()

print(f'PGPCA:\n PSNR: {psnr(ima, ima_fil_PGPCA):.2f} dB \n Computing Time: {end_time:.2f} s.')